Plot Model Components

Plotting power spectrum model parameters and components.

# Import the SpectralGroupModel object
from specparam import SpectralGroupModel

# Import utilities to manage frequency band definitions
from specparam.bands import Bands
from specparam.analysis import get_band_peak_group

# Import simulation utilities for making example data
from specparam.sim import sim_group_power_spectra
from specparam.sim.params import param_jitter

# Import plotting function for model parameters and components
from specparam.plts.periodic import plot_peak_fits, plot_peak_params
from specparam.plts.aperiodic import plot_aperiodic_params, plot_aperiodic_fits

Experiment Set Up & Simulate Data

In this example, we will explore the plotting functions available to visualize model parameters and components from fitting power spectrum models.

To do so, we will consider a hypothetical experiment in which we are compare power spectrum models between two groups of participants, and so we want to visualize differences between the groups. For simplicity, we will consider that we have one ‘grand average’ power spectrum per subject, which we can compare and visualize.

# Set up labels and colors for plotting
colors = ['#2400a8', '#00700b']
labels = ['Group-1', 'Group-2']

# Set the number of 'subjects' per group
n_subjs = 20

# Define the frequency range for our simulations
freq_range = [1, 50]

# Define aperiodic parameters for each group, with some variation
g1_aps = param_jitter([1, 1.25], [0.5, 0.2])
g2_aps = param_jitter([1, 1.00], [0.5, 0.2])

# Define periodic parameters for each group, with some variation
g1_peaks = param_jitter([11, 1, 0.5], [0.5, 0.2, 0.2])
g2_peaks = param_jitter([9, 1, 0.5], [0.25, 0.1, 0.3])

# Simulate some test data, as two groups of power spectra
freqs, powers1 = sim_group_power_spectra(n_subjs, freq_range, g1_aps, g1_peaks)
freqs, powers2 = sim_group_power_spectra(n_subjs, freq_range, g2_aps, g2_peaks)

Fit Power Spectrum Models

Now that we have our simulated data, we can fit our power spectrum models, using SpectralGroupModel.

# Initialize a SpectralGroupModel object for each group
fg1 = SpectralGroupModel(verbose=False)
fg2 = SpectralGroupModel(verbose=False)

# Parameterize neural power spectra
fg1.fit(freqs, powers1)
fg2.fit(freqs, powers2)

Plotting Parameters & Components

In the following, we will explore two visualization options:

• plotting parameter values

• plotting component reconstructions

Each of these approaches can be done for either aperiodic or periodic parameters.

All of the plots that we will use in this example can be used to visualize either one or multiple groups of data. As we will see, you can pass in a single group of parameters or components to visualize them, or pass in a list of group results to visualize and compare between groups.

You can also pass in optional inputs labels and colors to all the following functions to add plot labels, and to set the colors used for each group.

Periodic Components

First, let’s have a look at the periodic components.

To do so, we will use the Bands object to store our frequency band definitions, which we can then use to sub-select peaks within bands of interest.

We can then plot visualizations of the peak parameters, and the reconstructed fits.

# Define frequency bands of interest
bands = Bands({'theta' : [4, 8],
               'alpha' : [8, 13],
               'beta' : [13, 30]})

# Extract alpha peaks from each group
g1_alphas = get_band_peak_group(fg1, bands.alpha)
g2_alphas = get_band_peak_group(fg2, bands.alpha)

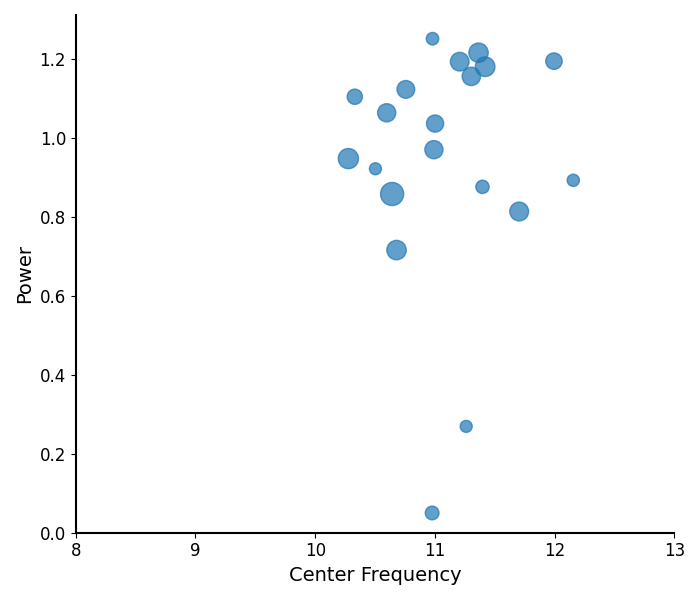
Plotting Peak Parameters

The plot_peak_params() function takes in peak parameters, and visualizes them, as:

• Center Frequency on the x-axis

• Power on the y-axis

• Bandwidth as the size of the circle

# Explore the peak parameters of Group 1's alphas
plot_peak_params(g1_alphas, freq_range=bands.alpha)

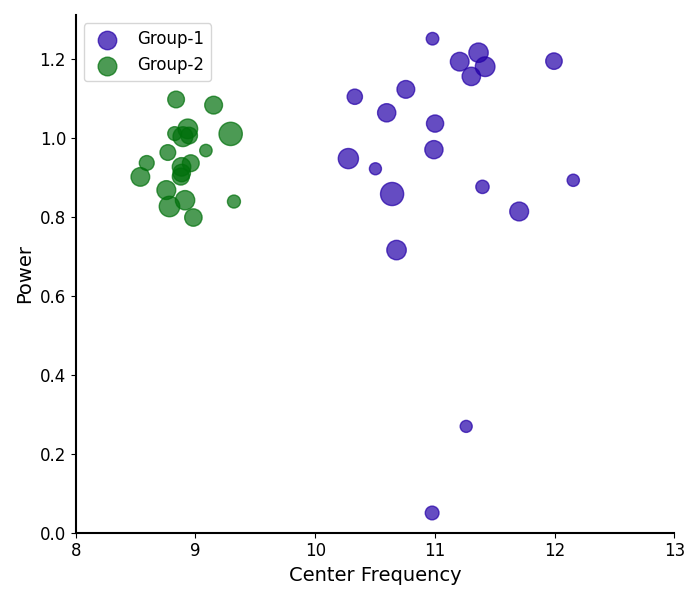
# Compare the peak parameters of alpha peaks between groups
plot_peak_params([g1_alphas, g2_alphas], freq_range=bands.alpha,
                 labels=labels, colors=colors)

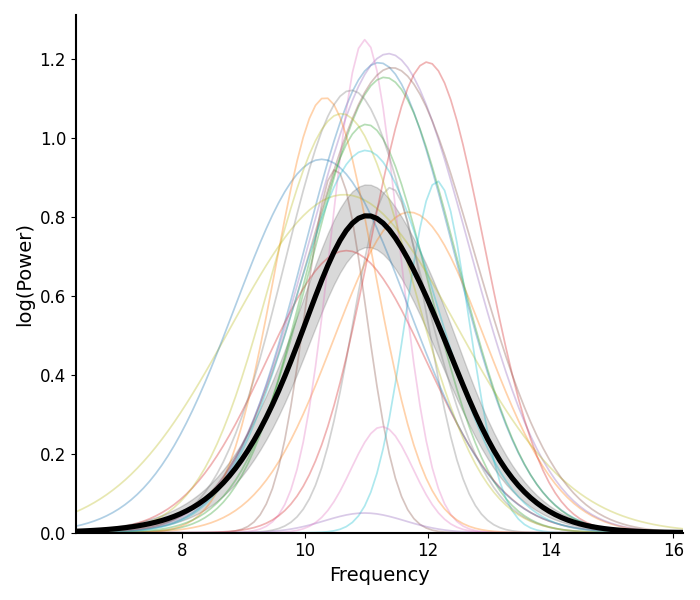
Plotting Peak Fits

The plot_peak_fits() function takes in peak parameters, and reconstructs peak fits.

# Plot the peak fits of the alpha fits for Group 1
plot_peak_fits(g1_alphas)

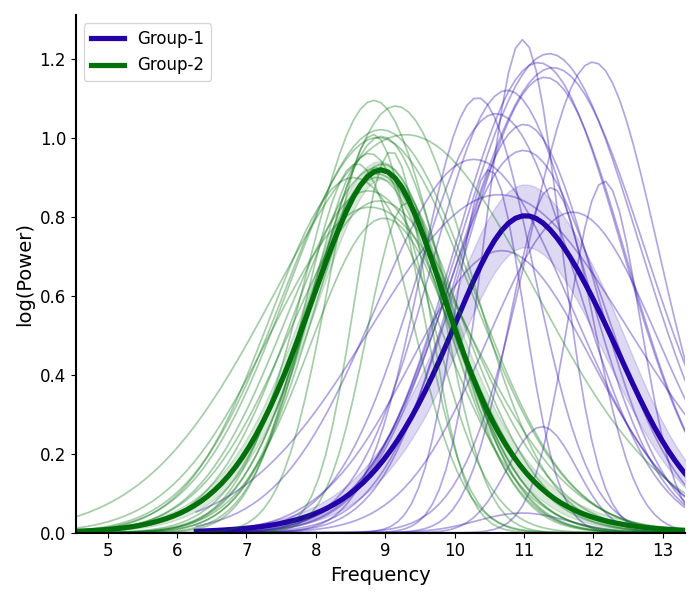
# Compare the peak fits of alpha peaks between groups
plot_peak_fits([g1_alphas, g2_alphas],
               labels=labels, colors=colors)

Aperiodic Components

Next, let’s have a look at the aperiodic components.

# Extract the aperiodic parameters for each group
aps1 = fg1.get_params('aperiodic_params')
aps2 = fg2.get_params('aperiodic_params')

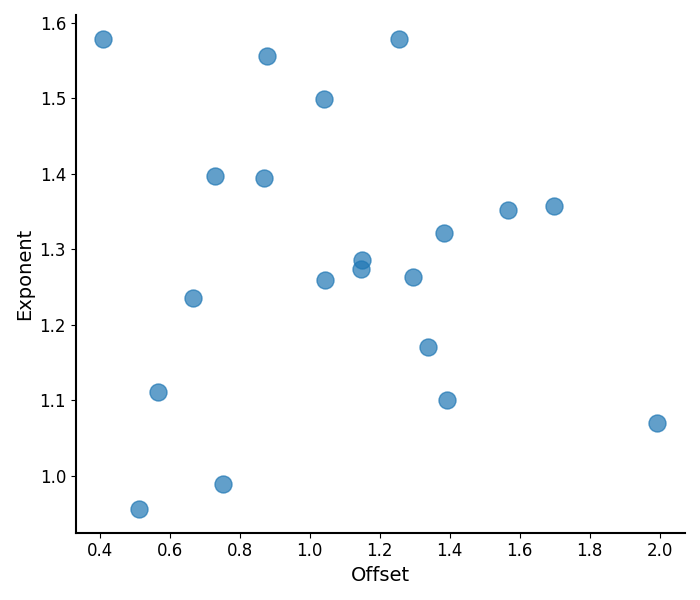
Plotting Aperiodic Parameters

The plot_aperiodic_params() function takes in aperiodic parameters, and visualizes them, as:

• Offset on the x-axis

• Exponent on the y-axis

# Plot the aperiodic parameters for Group 1
plot_aperiodic_params(aps1)

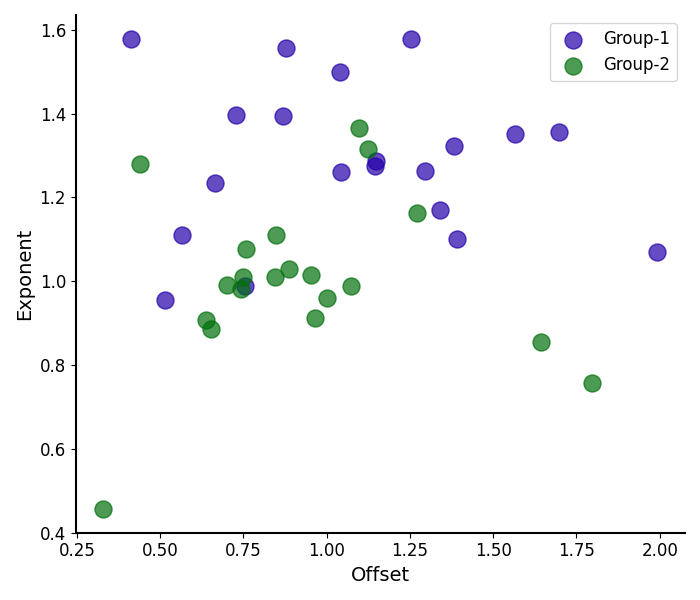
# Compare the aperiodic parameters between groups
plot_aperiodic_params([aps1, aps2], labels=labels, colors=colors)

Plotting Aperiodic Fits

The plot_aperiodic_fits() function takes in aperiodic parameters, and reconstructs aperiodic fits.

Here again we can plot visualizations of the peak parameters, and the reconstructed fits.

# Plot the aperiodic fits for Group 1
plot_aperiodic_fits(aps1, freq_range, control_offset=True)

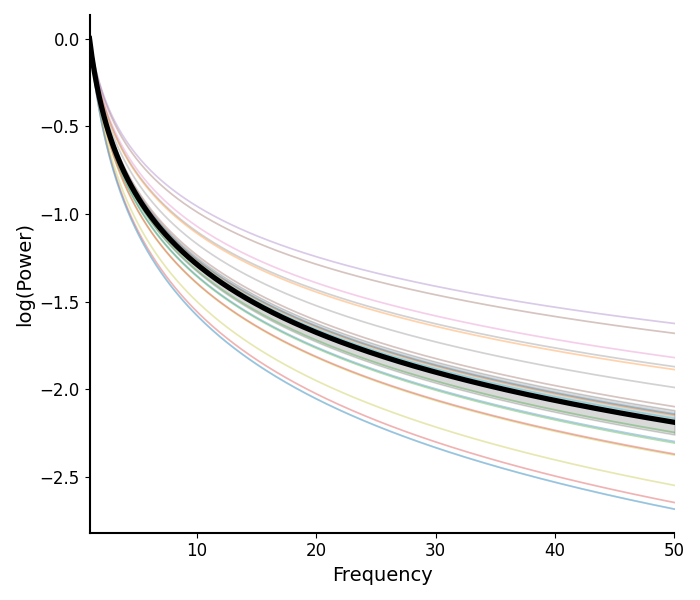
The plot_aperiodic_fits() also has some additional options that can help to tune the visualization, including:

• control_offset : whether the control for offset differences, by setting to zero

  • This can be useful to visualize if it’s the exponent specifically that is changing

• log_freqs : whether to log the frequency values, on the x-axis

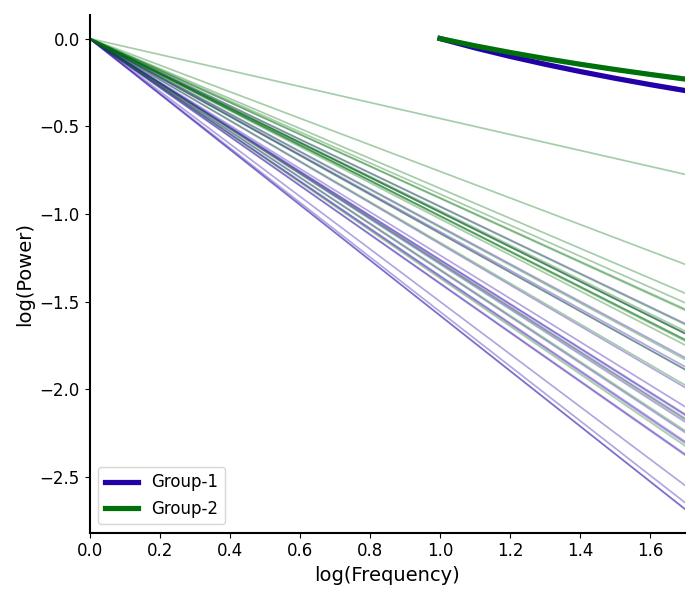
# Plot the aperiodic fits for both groups
plot_aperiodic_fits([aps1, aps2], freq_range,
                    control_offset=True, log_freqs=True,
                    labels=labels, colors=colors)

Conclusions

In this example, we explored plotting model parameters and components within and between groups of parameterized neural power spectra.

If you check the simulation parameters used for the two groups, you can see that we set these groups to vary in their alpha center frequency and in the exponent value. Qualitatively, we can see those differences in the plots above, and this (in real data) would suggest there may be interesting differences between these groups. Follow up analyses in such a case could investigate whether there are statistically significant differences between these groups.