Note
Go to the end to download the full example code.
04: Periodic Component Fitting¶
Choosing and using different modes for fitting the periodic component.
# Import the model object
from specparam import SpectralModel
# Import function to check available list of modes
from specparam.modes.definitions import check_modes
# Import a utility to download and load example data
from specparam.utils.download import load_example_data
Component Fit Modes¶
So far, we have initialized spectral fitting without explicitly specifying what model we want to fit the the data. By doing so, we have been using the default model definition.
However, we can also control which model forms we fit to the data, separately for the periodic and aperiodic components. This is done by explicitly specifying Fit Modes for each model component.
In this part of the tutorial, we will explore how this works for the periodic component.
Periodic Fitting Approaches¶
As we’ve already seen, to fit putatively periodic activity - operationalized as regions of power over above the aperiodic component - the model fits ‘peaks’.
However, in order to actually do this, we need to specify a mathematical definition of how to describe these peaks. Specifying this fit function is what is meant by choosing the periodic mode.
To see the available periodic fit modes, we can use the
check_modes() function.
# Check the list of periodic modes
check_modes('periodic')
Available periodic modes:
gaussian Gaussian peak fit function.
skewnorm Skewed Gaussian peak fit function.
cauchy Cauchy peak fit function.
Gaussian Periodic Mode¶
We will start with choosing the Gaussian fit mode.
# Download example data files needed for this example
freqs = load_example_data('freqs.npy', folder='data')
spectrum = load_example_data('spectrum.npy', folder='data')
# Initialize a model object, explicitly specifying periodic fit to 'gaussian'
fm1 = SpectralModel(periodic_mode='gaussian')
# Fit the model
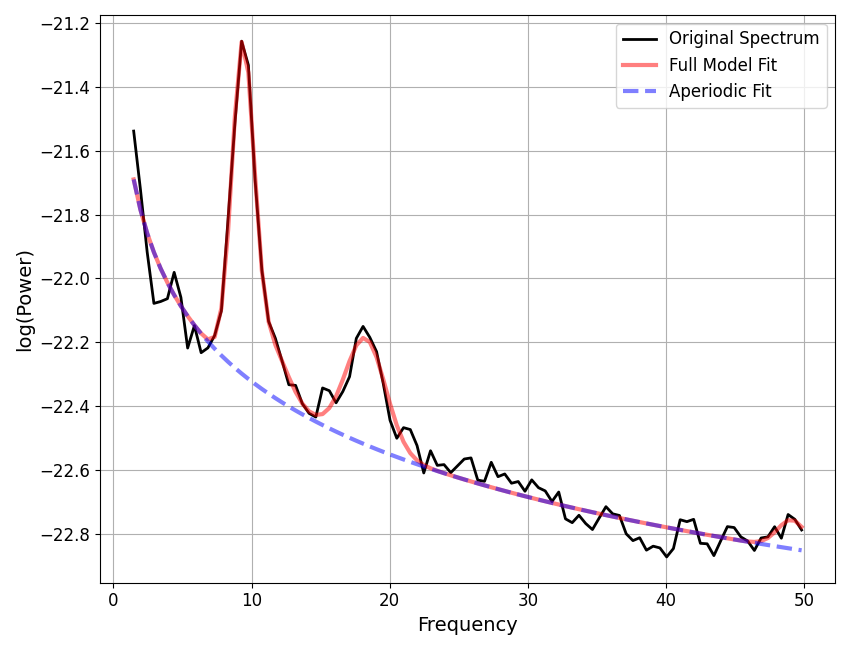
fm1.report(freqs, spectrum)
WARNING: Lower-bound peak width limit is < or ~= the frequency resolution: 0.50 <= 0.49
Lower bounds below frequency-resolution have no effect (effective lower bound is the frequency resolution).
Too low a limit may lead to overfitting noise as small bandwidth peaks.
We recommend a lower bound of approximately 2x the frequency resolution.
==================================================================================================
POWER SPECTRUM MODEL
The model was fit with the 'spectral fit' algorithm
Model was fit to the 1-50 Hz frequency range with 0.49 Hz resolution
Aperiodic Parameters ('fixed' mode)
(offset, exponent)
-21.5643, 0.7580
Peak Parameters ('gaussian' mode) 4 peaks found
CF: 9.37, PW: 1.04, BW: 1.58
CF: 11.26, PW: 0.23, BW: 2.65
CF: 18.26, PW: 0.33, BW: 2.89
CF: 49.12, PW: 0.09, BW: 2.08
Model fit quality metrics:
error (mae) is 0.0366
gof (rsquared) is 0.9831
==================================================================================================
Mathematical Description of the Periodic Component¶
You might notice that the above model looks the same as what we have fit previously. The Gaussian periodic mode is the default periodic mode.
Now that we have explicitly specified the Gaussian periodic fit mode, we can look into how the model is actually fit.
Each Gaussian, \(n\), referred to as \(G(F)_n\), is of the form:
This describes each peak in terms of parameters a, c and w, where:
\(a\) is the height of the peak, over and above the aperiodic component
\(c\) is the center frequency of the peak
\(w\) is the width of the peak
\(F\) is the array of frequency values
# Check the fit gaussian parameters
fm1.results.get_params('periodic', version='fit')
array([[ 9.36712112, 0.99082164, 0.78945133],
[11.26311335, 0.16434593, 1.32426813],
[18.25934079, 0.33386691, 1.44259837],
[49.11921998, 0.09105003, 1.03933721]])
Fit vs. Converted Parameters¶
You might notice in the above, where we printed out the periodic parameters, that in doing so we specified explicitly to get the ‘fit’ version of the parameters, and that these parameters are actually a bit different than the peak parameters reported in the report above.
This is because the model manages two version of each component parameters: - fit: which reflect the original fit parameters, that define the model - converted: which reflect parameters after any relevant conversions
The reason we may want to apply to conversions to the parameters is that the fit versions, while defining the model, may not reflect what we actually want to analyze as outputs.
# Check the fit gaussian parameters
fm1.results.get_params('periodic', version='converted')
array([[ 9.36712112, 1.03782895, 1.57890266],
[11.26311335, 0.22542876, 2.64853626],
[18.25934079, 0.33089465, 2.88519674],
[49.11921998, 0.08942602, 2.07867442]])
Converted Peak Parameters¶
The converted peak parameters are labeled as:
CF: center frequency of the extracted peak
PW: power of the peak, over and above the aperiodic component
BW: bandwidth of the extracted peak
The conversions that are applied to get these values are that:
CF is the exact same as mean parameter of the Gaussian
PW is the height of the model fit above the aperiodic component [1], which is not necessarily the same as the Gaussian height
BW is 2 * the standard deviation of the Gaussian [2]
[1] Since the Gaussians are fit together, if any Gaussians overlap, than the actual height of the fit at a given point can only be assessed when considering all Gaussians. To be better able to interpret heights for individual peaks, we re-define the peak height as above, and label it as ‘power’, as the units of the input data are expected to be units of power.
[2] Gaussian standard deviation is ‘1 sided’, where as the returned BW is ‘2 sided’.
Specifying a Different Fit Mode: Skewed Gaussian¶
As we saw above with check_modes there are also other periodic fit modes we can choose.
Next up, let’s try the skewed_gaussian mode.
# Initialize a model object, explicitly specifying periodic fit to 'gaussian'
fm2 = SpectralModel(periodic_mode='skewed_gaussian')
# Fit the model
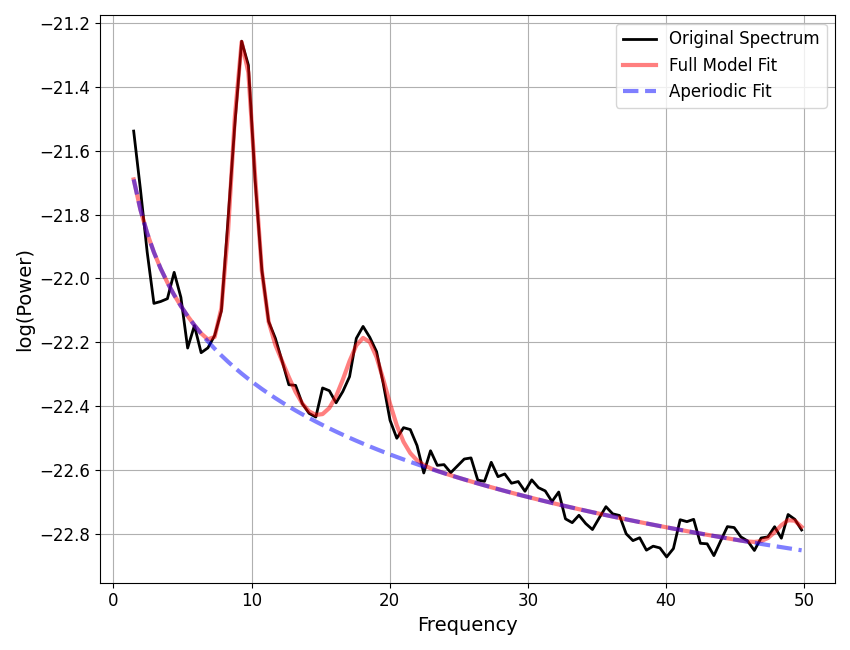
fm2.report(freqs, spectrum)
WARNING: Lower-bound peak width limit is < or ~= the frequency resolution: 0.50 <= 0.49
Lower bounds below frequency-resolution have no effect (effective lower bound is the frequency resolution).
Too low a limit may lead to overfitting noise as small bandwidth peaks.
We recommend a lower bound of approximately 2x the frequency resolution.
==================================================================================================
POWER SPECTRUM MODEL
The model was fit with the 'spectral fit' algorithm
Model was fit to the 1-50 Hz frequency range with 0.49 Hz resolution
Aperiodic Parameters ('fixed' mode)
(offset, exponent)
-21.5643, 0.7580
Peak Parameters ('skewnorm' mode) 4 peaks found
CF: 9.37, PW: 1.04, BW: 1.58, SKEW: -0.00
CF: 11.31, PW: 0.23, BW: 2.65, SKEW: -0.04
CF: 18.26, PW: 0.33, BW: 2.88, SKEW: 0.00
CF: 49.07, PW: 0.09, BW: 2.08, SKEW: 0.06
Model fit quality metrics:
error (mae) is 0.0366
gof (rsquared) is 0.9831
==================================================================================================
In the above, we can see that the peaks are fit a bit differently.
Note that the resulting parameters are also different.
Specifying a Different Fit Mode: Cauchy¶
Finally, we can try the remaining periodic mode, the cauchy distribution!
# Initialize a model object, explicitly specifying periodic fit to 'gaussian'
fm3 = SpectralModel(periodic_mode='cauchy')
# Fit the model
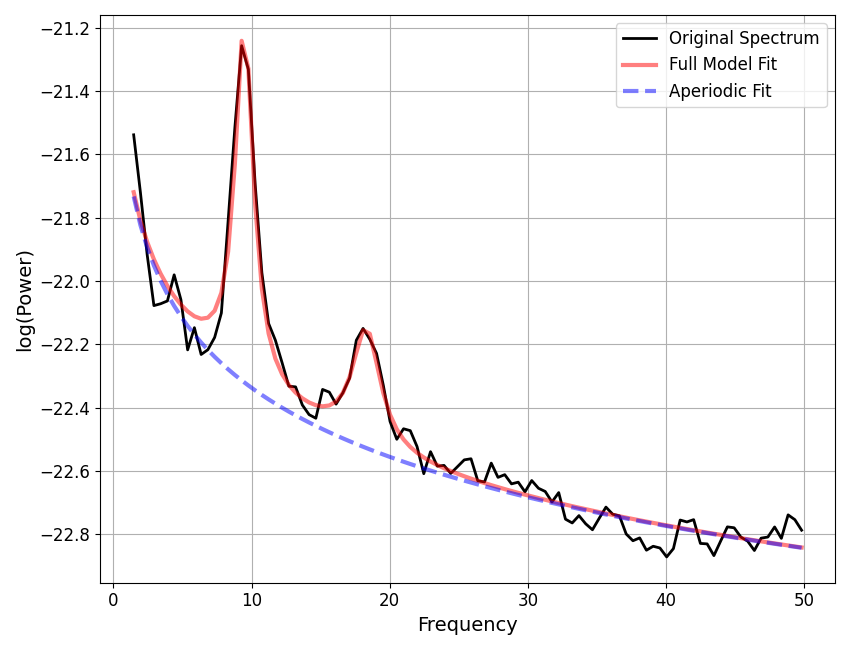
fm3.report(freqs, spectrum)
WARNING: Lower-bound peak width limit is < or ~= the frequency resolution: 0.50 <= 0.49
Lower bounds below frequency-resolution have no effect (effective lower bound is the frequency resolution).
Too low a limit may lead to overfitting noise as small bandwidth peaks.
We recommend a lower bound of approximately 2x the frequency resolution.
==================================================================================================
POWER SPECTRUM MODEL
The model was fit with the 'spectral fit' algorithm
Model was fit to the 1-50 Hz frequency range with 0.49 Hz resolution
Aperiodic Parameters ('fixed' mode)
(offset, exponent)
-21.6133, 0.7244
Peak Parameters ('cauchy' mode) 2 peaks found
CF: 9.47, PW: 1.07, BW: 1.62
CF: 18.30, PW: 0.37, BW: 2.48
Model fit quality metrics:
error (mae) is 0.0431
gof (rsquared) is 0.9772
==================================================================================================
That covers periodic mode selection!
Total running time of the script: (0 minutes 0.639 seconds)