Frequency-by-Frequency Errors

Check the error of power spectrum models across frequencies.

# Import numpy for some utility functions
import numpy as np

# Import model objects
from specparam import SpectralModel, SpectralGroupModel

# Import simulation utilities to create some test data
from specparam.sim import sim_power_spectrum, sim_group_power_spectra

# Import functions to examine frequency-by-frequency error of model fits
from specparam.analysis.error import compute_pointwise_error, compute_pointwise_error_group

Frequency-by-Frequency Error

When fitting power spectrum models, one of the goodness-of-fit measures computed and returned is the total error of th full model fit, compared to the original data.

Though potentially useful for evaluating overall performance, this total error measure doesn’t necessarily help to indicate where, in frequency space, or in what ways the model might be going wrong.

To get better insight into the model fitting, here we will explore some utilities that calculate and visualize the frequency-by-frequency error of model fits. This can allow for identifying where in the spectrum is being fit well, or not well.

Checking the Error of Individual Model Fits

First we will start by examining frequency-by-frequency error of an individual model fit, using simulated data.

The function for analyzing error from a model object is compute_pointwise_error(). To start with, we will indicate to this function to plot the frequency-by-frequency error of our model fit.

# Simulate an example power spectrum
freqs, powers = sim_power_spectrum([3, 50], [1, 1], [10, 0.25, 0.5])

# Initialize a model object
fm = SpectralModel(verbose=False)

# Parameterize our power spectrum
fm.fit(freqs, powers)

# Calculate the error per frequency of the model
compute_pointwise_error(fm, plot_errors=True)

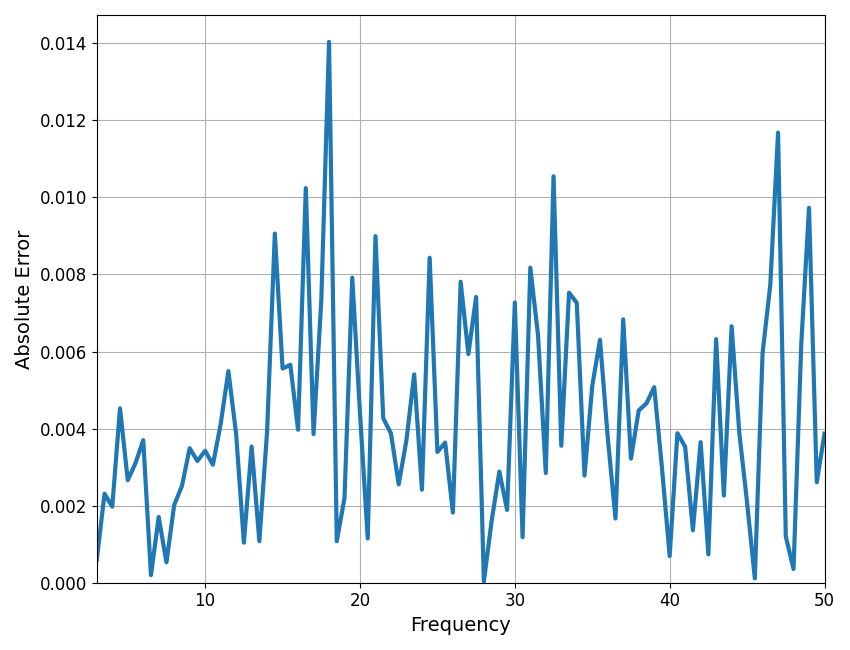
In the above, we can see that error is fairly even, and overall low. This suggests no particular problem with the fit.

You can also calculate and return the frequency-by-frequency errors of a model fit.

# We can also use this function to return the frequency-by-frequency error
errs_fm = compute_pointwise_error(fm, plot_errors=False, return_errors=True)

# Note that the average of this error is the same as the global error stored
print('Average freq-by-freq error:\t {:1.3f}'.format(np.mean(errs_fm)))
print('Model fit error: \t\t {:1.3f}'.format(fm.error_))

Average freq-by-freq error:      0.004
Model fit error:                 0.004

Checking the Error Across Groups of Model Fits

Next, lets move on to calculating frequency-by-frequency error across groups of fits, again using some simulated data.

To analyze error from a SpectralGroupModel object, use compute_pointwise_error_group().

# Simulate a group of power spectra
freqs, powers = sim_group_power_spectra(10, [3, 50], [1, 1], [10, 0.3, 1], nlvs=0.1)

# Initialize a SpectralGroupModel object to fit
fg = SpectralGroupModel(min_peak_height=0.25, verbose=False)

# Parameterize our group of power spectra
fg.fit(freqs, powers)

Just as before, we can plot and/or return the error.

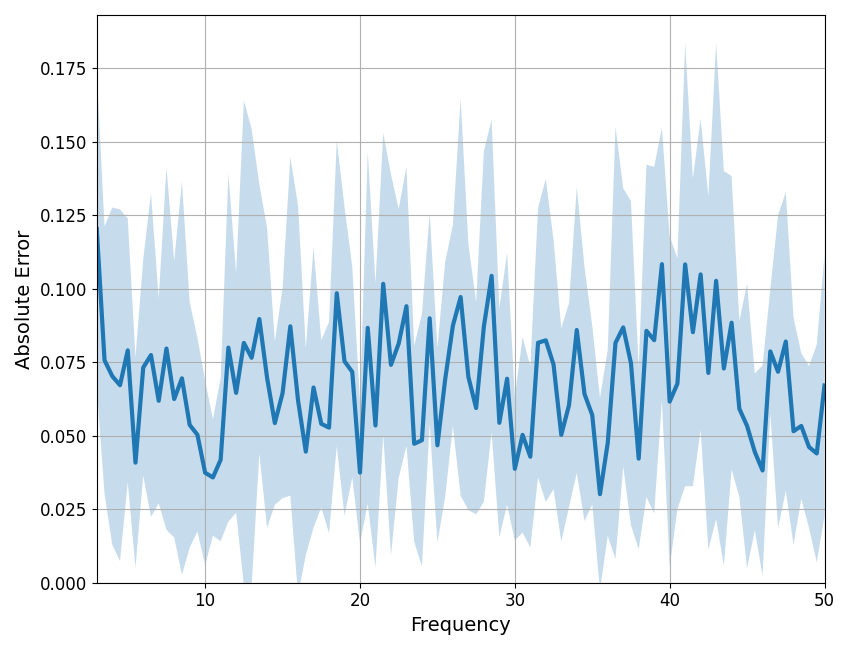
When plotting the error, the plot line is the mean error per frequency, across fits, and the shading indicates the standard deviation of the error, also per frequency.

# Plot the group frequency-by-frequency error
compute_pointwise_error_group(fg, plot_errors=True)

# Return the errors - this returns a 2D matrix of errors for all fits
errs_fg = compute_pointwise_error_group(fg, False, True)

# We can check which frequency has highest error, or standard deviation of error
f_max_err = fg.freqs[np.argmax(np.mean(errs_fg, 0))]
f_max_std = fg.freqs[np.argmax(np.std(errs_fg, 0))]

# Print out frequency of maximal error
print('Frequency with highest mean error: \t\t\t', f_max_err)
print('Frequency with highest standard deviation of error: \t', f_max_std)

Frequency with highest mean error:                       3.0
Frequency with highest standard deviation of error:      12.5

In the plot and checks above, we again see that the error is on average low, and that there is no region that stands out as problematic.

Frequency-by-Frequency Errors When There is a Problem

So far we have examined cases in which the models were working well, and the frequency-by-frequency error revealed no big surprises.

As a final example, let’s examine a case in which the model is not working well, and see how the errors look. In particular, we will simulate some new power spectra, with a knee parameter, and refit with the same SpectralGroupModel object, in ‘fixed’ aperiodic mode, and then analyze the frequency-by-frequency errors, as before. In this scenario, we are fitting data with the wrong model form, and so we expect there to be some issues with the fit, and we can use the frequency-by-frequency error to investigate if and how this is the case.

# Simulate a group of power spectra, with a knee
freqs, powers = sim_group_power_spectra(10, [1, 50], [0, 10, 2],
                                        [10, 0.3, 1], nlvs=0.01)

# Parameterize our new group of power spectra
fg.fit(freqs, powers)

# Plot the group frequency-by-frequency error
compute_pointwise_error_group(fg, plot_errors=True)

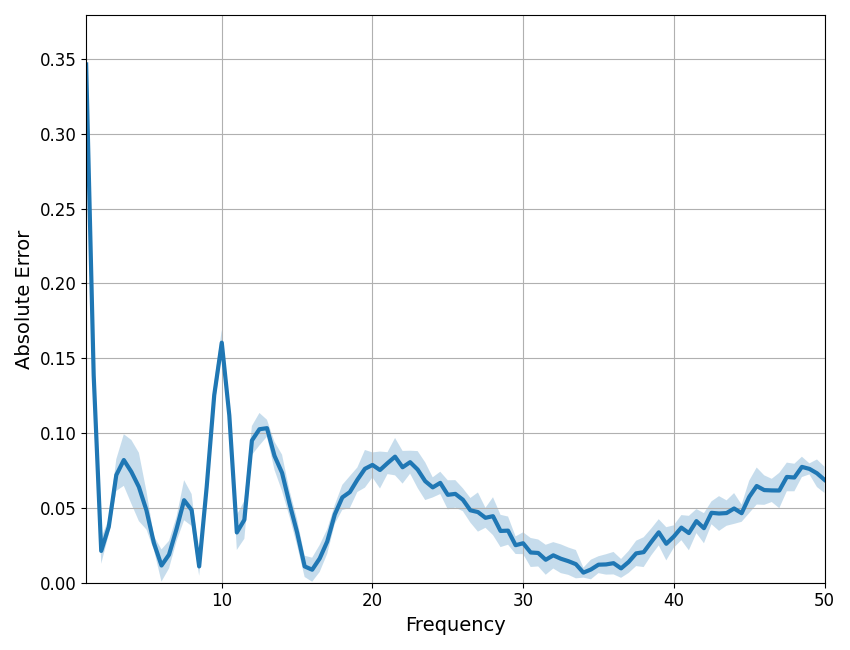
In the plot above, we can see that there is more error in the model, but also that this error is not evenly distributed. The error is uneven across frequencies, and particularly high around the low frequencies. In this case, this is due to a mismatch between the data properties we simulated and the aperiodic mode used to fit the data.

If you see high errors, especially bunched up around particular frequencies, this is a sign that something might be going wrong, and it might be worth looking more into the how the model fits are going.